This is part two of a three part series analyzing The Day of the Tentacle:
This post is an analysis of the Puzzle Dependency Graph.
The Day of the Tentacle is a classic LucasArts adventure game released in 1993. Starring an irrepressible nerd, an evil tentacle and three generations of the same mad scientist it quickly captured the hearts of the adventure going public of the day. It’s a light-hearted game with a focus on exploration, narrative and humor. The creative team included Dave Grossman, Tim Schafer, Ron Gilbert and Gary Winnick.
While cartoonish on the surface this game is highly polished with an elaborate design and complex puzzle structure. This post will focus on the puzzle dependency graph and the way in which the puzzles are integrated into the narrative.
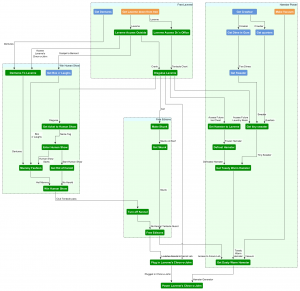
Puzzle Dependency Graph
For the purpose of analyzing the game I have re-constructed the Puzzle Dependency Graph as described in Part 1: Puzzle Dependency Graph Primer. I used yEd to build the graph and CAM for the GANTT chart. The graph is laid out vertically from top to bottom with nodes colored to show which game character is required to solve the puzzle. The colors are assigned as follows:
| Bernard: Blue | Laverne: Green | Hoagie: Orange | Start / End |
Nodes were created for all player actions which satisfy downstream dependencies. I did not create nodes for the act of just picking up an item which is lying around or for walking into new areas. While those actions technically fit the criteria it is usually an earlier puzzle which has actually allowed the player to take that action and so the dependencies are assigned to those upstream puzzles.
As recommended in Part 1 I have used a layout which places puzzles in the highest layer possible while still keeping all dependencies flowing downwards. Note that the three graphs shown in this post all represent the same dependency graph data but with different layouts. The initial graph with no grouping of nodes is shown here.
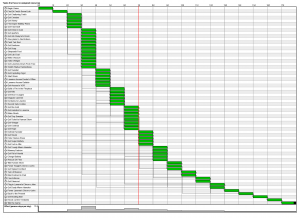
Dependency Graph displayed using a compact layout. The non-linear mid-game is kicked off dramatically by the “Find Super Battery Plans” puzzle with its 15 downstream puzzles.
Features of the Graph
In this graph there is a single initial starting node with no input edges (the starting condition) and one destination node which has no outbound edges (the victory condition). The horizontal layers give an indication of the amount of non-linear branching happening at a given point in the game. When all the puzzles of a layer are completed then all the puzzles in the next layer down are guaranteed to have their dependencies satisfied and are available for solving. Of course the player need not solve all puzzles layer-by-layer and so the number of puzzles available at a given time could be more or less than the number in a particular branch. The size of the layer just gives us general idea of the degree of non-linear branching at each phase of the game.
A valid order in which the player may solve the puzzles is known as a Topological Order. Due to the high degree of non-linear branching this game has a vast number of valid topological orders. The exact number is not known to me but a lower bound can be determined by looking at the number of permutations possible in the largest layer. With 13 puzzles in the fourth layer there are over 6.2 billion possible orders in which the player might solve them.
The GANTT chart is a nice way to look at the size of the layers visually. It shows the number of puzzles available in each layer as green boxes in vertical columns. From this we can see that this game has a short linear introductory segment followed by a very non-linear middle-game with all kinds of puzzles available for solving at once. The degree of non-linear branching is reduced slowly as the game winds down and finishes with a completely linear segment of 4 puzzles at the end.
Other games could have dependency graphs with different features. A game with multiple starting conditions would have more than one initial node in the first layer. A game with multiple victory conditions or optional puzzles which do not contribute to the final victory would have more than one leaf node.
The shapes of the dependency graph and the GANTT chart are also instructive. A game which was purely linear would have a straight line of nodes from start to finish, each with one dependency. If there was an even higher degree of non-linear branching the result would be a wider graph with more puzzles in each individual layer. This game follows the advice of Noah Falstein when he said “Make it Bushy“. By this he is advocating for a graph which balances linear and non-linear branching into a shape that resembles a bush. This shape is also mentioned by Ron Gilbert when talking about the graph for his current game “Thimbleweed Park”.
Considering these other possible types of graphs allows us to think about how The Day of the Tentacle was constructed. Choices were clearly made by the designers to incorporate every puzzle into the narrative and to have no “alternate” endings or even optional “easter-egg” puzzles. The focus on non-linearity gives the player plenty of available puzzles in the mid-game. This has the benefit of giving plenty of things to do at any time and avoids holding up the game because the player is stuck on a single puzzle. This choice had to be carefully crafted into the game however. Many games begin to feel aimless and random when there are too many possibilities with no clear goal. Day of the Tentacle manages to retain the benefits of non-linearity while avoiding the pitfalls and this is in large part due to the puzzle structure.
Character Cooperation
A key game device of The Day of the Tentacle is the ability to switch between characters. This is somewhat unusual in adventure games and very unusual in that it actually works from a gameplay and story perspective. Most games which require the player to juggle multiple characters don’t work nearly as well (including Maniac Mansion). One reason I think it succeeds is the combination of the time-travel as a narrative device and the restriction of the setting to different versions of the same Mansion. These two elements combine to enable many cooperative puzzles where one character’s actions contribute to a puzzle for another. This is done by passing items via the Chron-o-Johns and by taking actions in the past which affect the future. It’s a testament to the high caliber design of this game that these two basic actions are used over and over but they never seem to lose their charm or magic.
Swimlanes
We can tell exactly how many puzzles involve this kind of inter-character cooperation by looking at the Dependency Graph grouped into lanes. Each lane groups the puzzles solved by an individual character. If we look at the edges between nodes which cross from one lane into another we can easily see which puzzles have dependencies on other characters’ puzzles. There are 32 of these types of inter-dependent puzzles. Half of the gameplay therefore relies on either cooperating directly between characters via the Chron-o-Johns or taking some action with one character with enables a puzzle for another character (usually crossing time). The Dependency Graph is shown here separated into lanes:
Dependency Graph grouped into “swimlanes” by character. Puzzles which require cooperation between characters can be seen by the edges which cross between lanes.
Expanding and Contracting
There is more that we can discover by analyzing the graph. Looking at the in and out degrees on each node we can see which puzzles open up or close down the branching and by what degree. It is clear that the puzzles which open up the branching in this game really open it up. Find the Super Battery Plans opens up 15 downstream puzzles. The player spends the rest of the game finding and closing down all those branches. The puzzles which close it down generally reduce the branching by only 1 or 2 (meaning their in-degree is only 1 or 2 more than their out-degree). This is certainly a design choice and it would be interesting to know if other approaches were tried and discarded.
| Puzzle | In Degree | Out Degree |
|---|---|---|
| Find Super Battery Plans | 1 | 15 |
| Disguise Laverne | 2 | 6 |
| Find Dr. Fred’s secret lab | 1 | 6 |
| Laverne Access Outside | 1 | 3 |
| Get Laverne down from tree | 1 | 2 |
| Enter Human Show | 1 | 2 |
| Get Crowbar | 1 | 2 |
| Puzzle | In Degree | Out Degree |
|---|---|---|
| Get the Super Battery | 4 | 1 |
| Mummy Fashion | 4 | 1 |
| Get tiny sweater | 3 | 1 |
| Get Dusty Warm Hamster | 3 | 1 |
| Back to the Present | 3 | 1 |
| Get Vinegar | 2 | 1 |
| Build a fire | 2 | 1 |
| Start Storm | 2 | 1 |
| Get lab coat | 2 | 1 |
| Get Kite | 2 | 1 |
| Charge Battery | 2 | 1 |
| Dentures to Laverne | 2 | 1 |
| Get Rid of Harold | 2 | 1 |
| Win Human Show | 2 | 1 |
| Get Skunk | 2 | 1 |
| Plug in Laverne’s Chron-o-John | 2 | 1 |
| Get Toasty Warm Hamster | 2 | 1 |
| Power Laverne’s Chron-o-John | 2 | 1 |
| Rescue Dr. Fred | 2 | 1 |
| Get Signed Contract | 2 | 1 |
| Mail Contract In Past | 2 | 1 |
Narrative Structure
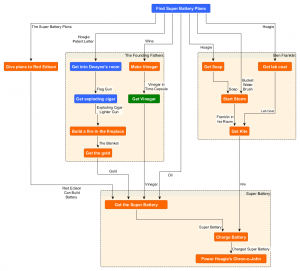
As discussed in the Puzzle Dependency Graph Primer, non-linear branching in the puzzle structure poses complications for narrative. This is because of the factorial expansion of the orders in which the player may solve the puzzles. The Day of the Tentacle addresses this problem by isolating the narrative sub-plots into almost totally distinct puzzle trees. We can see this very clearly by organizing the puzzle dependency graph into groups based on the downstream goal. This graph shows this.
The non-linear branching of puzzles in The Day of the Tentacle aligns closely with the major sub-plots of the game. Only a single cross dependency exists between groups.
It is clear from the graph that there are essentially three totally separate games here which map directly to the primary sub-plots. We can see that it is possible to play through the entire sub-tree to ‘Power Laverne’s Chron-o-John’ without ever doing any of the puzzles in either of the other two sub-trees. Likewise we can ‘Get the Diamond’ without doing a single puzzle outside of that sub-tree. There is only one puzzle which has a dependency outside its group. That is “Get Vinegar” which requires “Access to the History Room” from the “Dentures to Laverne” puzzle. This acts like a gate which requires the player to at least get Laverne down from the tree and disguised before Hoagie can continues on to the end of his story. There are more of these gates internal to each story tree which we will explore below.
The fact that the game is broken up into these three siloed sub-plots is completely masked by the character switching dynamic. Since all of the sub-plots require extensive cooperation between characters it never feels like you are working on an isolated puzzle group. Also, given the vast number of orders in which the puzzles can be solved, the player is very unlikely to resolve one plot completely before even starting another one anyway. This is great for the player experience as they are free to make progress on all three sub-goals at any time. So if it is not noticeable to the player what is the point of keeping these puzzles all in their own sub-graphs?
From a narrative standpoint keeping the sub-plots isolated seems to be the key to maintaining a coherent story regardless of the order the puzzles are solved. With 13 puzzles in the fourth layer there are over 6 billion possible orders in which the player may solve them. To attempt to turn each order into a coherent story is obviously impossible. The solution The Day of the Tentacle takes is to isolate the subplots and then even further divide them into very small sub-trees which are able to be solved essentially linearly.
Sub-dividing the puzzles is only part of the equation, however. It is interesting to note that the dialogue and NPC actions which go along with the puzzles in each subplot do not reference any of the other subplots. The puzzles and plot points which together make up a sub-plot are completely self-contained and coherent regardless of what other units the player has or has not also experienced.
So we can see that two design choices were made. First: breaking up the puzzles and narrative into distinct units and second: refrain from making any narrative references to information outside of the unit. These both seem to be fundamental to the way Day of the Tentacle can provide a high degree of non-linear branching without introducing lots of logical narrative “bugs” or an impossible maze of dialogue trees to account for the different orders the player may visit the stories in.
A Detailed Example: Hoagie’s Journey
To demonstrate this design feature of narrative isolation I will walk through Hoagie’s narrative from the beginning of the game through to the point he plugs in his Chron-o-John. Then we can review how the narrative is broken into isolated sub-plots and compare the relevant sub-trees in the dependency graph to see how they relate.
The Story Begins
Purple tentacle drinks toxic sludge, turns mutant and decides to take over the world. So Dr. Fred ties up the tentacles in his secret lab and is planning to kill them both. The hamster goes to Bernard’s house to warn Bernard who decides to rescue the tentacles, bringing his two friends Hoagie and Laverne along.
After arriving at the house the kids split up. Bernard discovers the secret lab and releases the tentacles at which point Dr. Fred shows up and reminds Bernard that Purple Tentacle is incredibly evil and is planning on taking over the world. The only hope is to turn off the sludge-o-matic yesterday by using the time machine. So Bernard, Hoagie and Laverne travel through time in the chron-o-johns but due to an immitation Diamond the machine malfunctions. Bernard ends up back in the present, Hoagie goes 200 years in the past and Laverne is 200 years in the future. Now the goal shifts to rescuing the two friends.
With instructions from Dr. Fred Bernard realizes he must get a real diamond to use in the time machine and figure out a way for Hoagie and Laverne to plug in their Chron-o-Johns. Since Hoagie is 200 years in the past the only way for him to do that is to use Dr. Fred’s patented super battery. Dr. Fred flushes the plans for the battery down the Chron-o-John which sends them through time to Hoagie. Dr. Fred instructs him to take the plans to his long distant ancestor Red Edison.
The Floundering Founding Fathers
Red Edison tells Hoagie he can make the super battery if he has Oil, Vinegar and Gold. The oil is found in the kitchen but the other items need more work. Hoagie discovers that the Founding Fathers are holed up in the mansion trying to write the Constitution but they have writer’s block and aren’t making much progress. There is a gold quill on the table but they won’t let Hoagie grab it. Jefferson does have a time capsule though – Hoagie puts a bottle of wine in the time capsule in order to send it to the future to make vinegar. By giving George Washington an exploding cigar, Hoagie knocks out his teeth which he replaces with the chattering teeth from the present day mansion. This makes George look cold and so Jefferson starts a fire in the fireplace. Hoagie puts the blanket Hancock was wearing on the top of the chimney, filling the room with smoke and setting off the fire alarm. The founding fathers all jump out the window which gives Hoagie a chance to snag the gold quill.
Once Laverne gets access to the history room in the future she is able to get the vinegar and send it back to Hoagie. Then, with oil, vinegar and gold he returns to Red Edison’s basement lab and hands them over to Red Edison who constructs a Super Battery out of them. However the super battery needs to be charged before it can power his chron-o-john.
The Ben Franklin Experience
After finding Ben Franklin in a field trying to discover electricity Hoagie realizes that he might be able to power his Super Battery if Ben got his experiment to work. But it’s too sunny for a storm so he collects a brush, a bucket, soap and water and washes the buggy out in front of the house in order to make it rain. Unfortunately this just makes Franklin go back in the house because his kite won’t work if it gets wet. So he gives Red Edison the Help Wanted sign from the present day and gets hired as a “moronic drone”. This has the benefit of giving him access to a lab coat which Franklin then cuts up and makes an All-Season Frank-o-Copter which can fly in the rain. They both go back out to the field where Hoagie slips the Super Battery into the kite and when it gets hit by lightning the battery is charged.
Deconstructing Hoagie
There are three main story threads involved in getting Hoagie back to the present:
- Building and Charging The Super Battery
- The Founding Fathers
- Ben Franklin
These three stories branch out from the same incident – Hoagie traveling to the past – and they come back together with Hoagie getting the Super Battery, charging it and plugging it into his Chron-o-John. In between these two events the stories diverge into their own sub-plots. If we follow the inverted dependency trees back upwards from ‘Get the Super Battery’ we can see that the puzzles also exist in isolated sub-graphs. So it is possible to Get the Gold without making any progress down another tree. Likewise it is possible to Get the Kite or the Vinegar without having even given the plans to Red Edison.
The key thing to note here is that none of the dialogue in the narrative around these three stories makes any assumptions about what the player has done outside of the small sub-plot in question. Hoagie never mentions ‘Oh great I need this gold to get the Super Battery’, or ‘I bet I can charge the Super Battery with this Kite’. This is because the player may not even have given the plans to Red Edison before getting the Gold or getting the Kite. So they may not even know what ingredients are required or that the battery will need charging. By restricting any references in the dialogue and action to the puzzles and stories of each small sub-graph the game has avoided those kinds of “bugs” in the story.
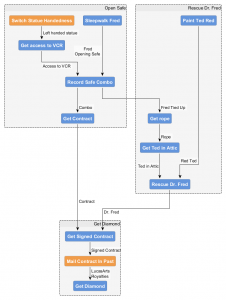
Bernard’s Journey
Both Bernard and Laverne’s stories use a similar mechanism. Bernard’s is the simplest with two serial sub-plots and a maximum of three puzzles in a single layer. Bernard’s goals are to Get the Contract, Rescue Dr. Fred from the IRS and then Get the Diamond. Bernard’s story differs from Hoagie’s in that these parts are linear and must happen in sequence. This is enforced by two gated sections where you can’t get the rope until you have opened the safe and you can’t get the signed contract until you rescue Dr. Fred. So Bernard’s subplots essentially form a single serial narrative which have no possibility of having narrative information incorrectly referenced out of order.
Laverne The Great
Laverne’s story is much different. It is the longest and most complicated with four sub-plots and the biggest puzzle group of the game. Her subplots are:
- Gain her freedom
- Win the Human Show
- Free the Edisons
- Power the Chron-o-John using a Hamster
Before Laverne is disguised and can freely roam around the future mansion there are puzzles to be solved which eventually will play into her narrative but which are not motivated by anything. For example it is likely that the player will get the sweater out from under the sleeping conventioneer without knowing at the time what it will be used for. This is an example of a ‘key before the lock’ puzzle and can lead to player confusion (see reference to Ron Gilbert’s rules for adventure games in Part 3). In fact the need for the hamster (frozen, warm, dusty or otherwise) is not motivated at all until Laverne gets into the basement and finds the generator. So the number of puzzles which the player may solve “just because” is quite large.
Winning the Human Show on the other hand is well set up and has a number of clear guideposts in the narrative. This subplot is encapsulated and can be solved from start to finish with no outside dependencies. Once her two sub-plots are completed she can resolve her primary story and power her chron-o-john and get back to the present where the kids gang up and resolve the over-arching plot by saving the world from Purple Tentacle (and getting out of Dr. Fred’s house).
Summary
We have seen how the puzzles and narrative are broken down into three almost totally isolated groups and how each of those is broken further down into little sub-plots which are themselves well encapsulated with minimal external narrative references. By doing this the design of this game seems to have been greatly simplified. Instead of attempting to write dialogue and actions around a vast number of possible story scenarios based on the order the player might solve puzzle in the problem is reduced down to simple linear story-telling within the sub-plots. I believe this is the key to how The Day of the Tentacle benefits from a high degree of non-linear branching – effectively allowing the player to choose the order in which the story is told – while still avoiding mistakes where a reference is made to an event the player has not yet experienced.
Files
If you are interested in doing your own exploration of the dependency graph, here is the graph in various formats:
- Day of the Tentacle Dependency Graph – in swimlanes grouped by character: (yEd) (PNG)
- Day of the Tentacle Dependency Graph – grouped by sub goal: (yEd) (PNG)
Feel free to make use of these files in your own research. If you publish something I would love a link to it. Thank you.